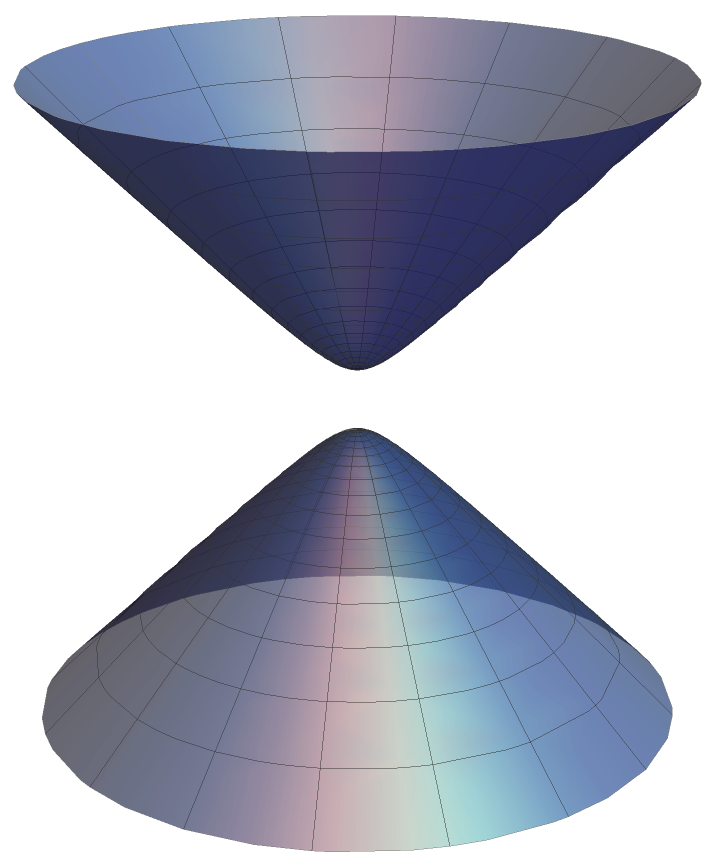
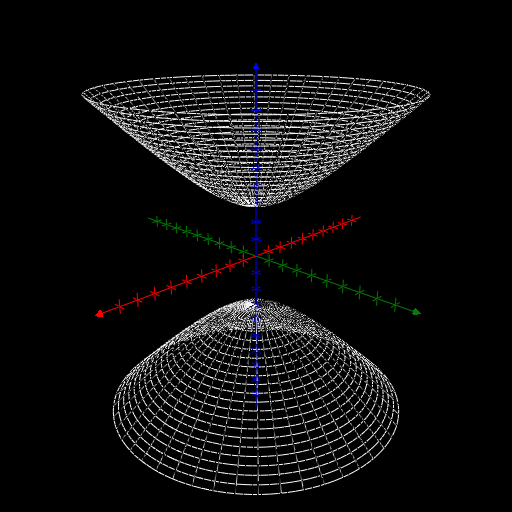
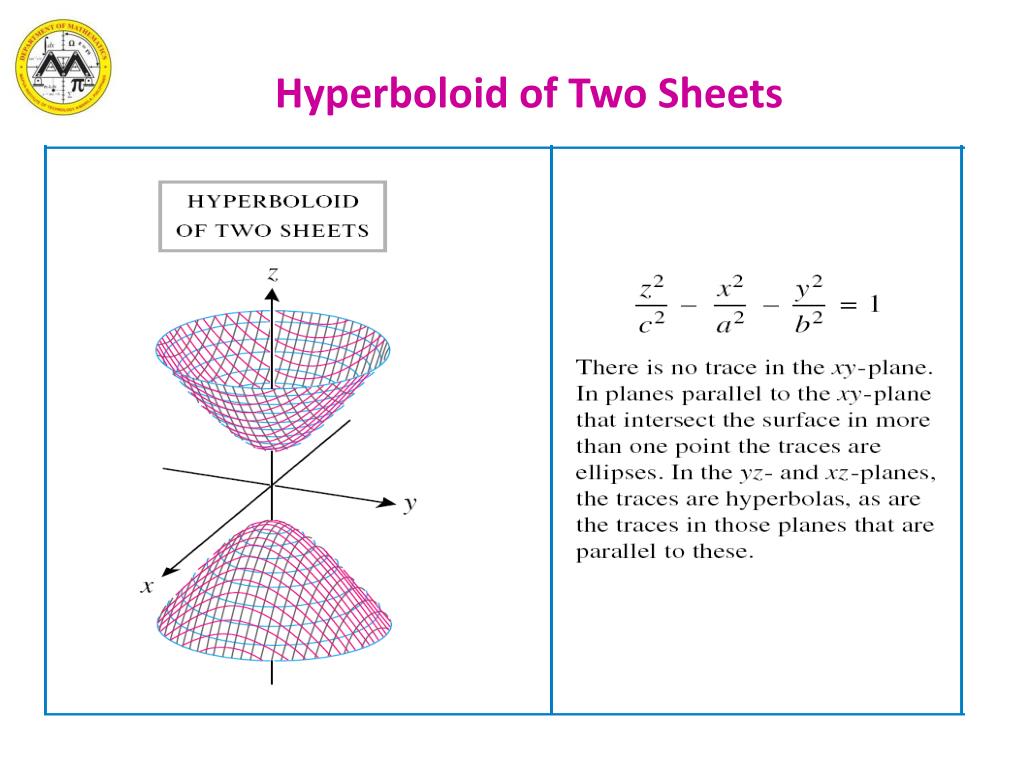
Hyperboloid Of 2 Sheets - The first one is hyperboloid in one sheet. You will get two negative letter terms. Let us say that we have a quadric equation, whose solution set lies in $\mathbb{r}^3$, and you know it's a. Find the parametrization for the hyperboloid of two sheets${(x,y,z) \in \mathbb{r}^3};
You will get two negative letter terms. Let us say that we have a quadric equation, whose solution set lies in $\mathbb{r}^3$, and you know it's a. Find the parametrization for the hyperboloid of two sheets${(x,y,z) \in \mathbb{r}^3}; The first one is hyperboloid in one sheet.
You will get two negative letter terms. The first one is hyperboloid in one sheet. Find the parametrization for the hyperboloid of two sheets${(x,y,z) \in \mathbb{r}^3}; Let us say that we have a quadric equation, whose solution set lies in $\mathbb{r}^3$, and you know it's a.
TwoSheeted Hyperboloid from Wolfram MathWorld
The first one is hyperboloid in one sheet. You will get two negative letter terms. Find the parametrization for the hyperboloid of two sheets${(x,y,z) \in \mathbb{r}^3}; Let us say that we have a quadric equation, whose solution set lies in $\mathbb{r}^3$, and you know it's a.
Hyperboloid of Two Sheet
Let us say that we have a quadric equation, whose solution set lies in $\mathbb{r}^3$, and you know it's a. You will get two negative letter terms. The first one is hyperboloid in one sheet. Find the parametrization for the hyperboloid of two sheets${(x,y,z) \in \mathbb{r}^3};
Hyperboloid of TWO Sheets
Let us say that we have a quadric equation, whose solution set lies in $\mathbb{r}^3$, and you know it's a. Find the parametrization for the hyperboloid of two sheets${(x,y,z) \in \mathbb{r}^3}; You will get two negative letter terms. The first one is hyperboloid in one sheet.
hyperboloid of two sheet
Let us say that we have a quadric equation, whose solution set lies in $\mathbb{r}^3$, and you know it's a. Find the parametrization for the hyperboloid of two sheets${(x,y,z) \in \mathbb{r}^3}; The first one is hyperboloid in one sheet. You will get two negative letter terms.
Hyperboloid of two sheets The Rejbrand Encyclopædia of Curves and
The first one is hyperboloid in one sheet. You will get two negative letter terms. Let us say that we have a quadric equation, whose solution set lies in $\mathbb{r}^3$, and you know it's a. Find the parametrization for the hyperboloid of two sheets${(x,y,z) \in \mathbb{r}^3};
Graphing a Hyperboloid of Two Sheets in 3D YouTube
Let us say that we have a quadric equation, whose solution set lies in $\mathbb{r}^3$, and you know it's a. The first one is hyperboloid in one sheet. Find the parametrization for the hyperboloid of two sheets${(x,y,z) \in \mathbb{r}^3}; You will get two negative letter terms.
hyperboloid of two sheet
Let us say that we have a quadric equation, whose solution set lies in $\mathbb{r}^3$, and you know it's a. The first one is hyperboloid in one sheet. Find the parametrization for the hyperboloid of two sheets${(x,y,z) \in \mathbb{r}^3}; You will get two negative letter terms.
Mathematics Textbook Illustration Portfolio gallery of Mathematics
Let us say that we have a quadric equation, whose solution set lies in $\mathbb{r}^3$, and you know it's a. You will get two negative letter terms. Find the parametrization for the hyperboloid of two sheets${(x,y,z) \in \mathbb{r}^3}; The first one is hyperboloid in one sheet.
PPT MATH23 MULTIVARIABLE CALCULUS PowerPoint Presentation, free
Let us say that we have a quadric equation, whose solution set lies in $\mathbb{r}^3$, and you know it's a. Find the parametrization for the hyperboloid of two sheets${(x,y,z) \in \mathbb{r}^3}; You will get two negative letter terms. The first one is hyperboloid in one sheet.
Quadric Surface The Hyperboloid of Two Sheets YouTube
You will get two negative letter terms. The first one is hyperboloid in one sheet. Let us say that we have a quadric equation, whose solution set lies in $\mathbb{r}^3$, and you know it's a. Find the parametrization for the hyperboloid of two sheets${(x,y,z) \in \mathbb{r}^3};
You Will Get Two Negative Letter Terms.
The first one is hyperboloid in one sheet. Let us say that we have a quadric equation, whose solution set lies in $\mathbb{r}^3$, and you know it's a. Find the parametrization for the hyperboloid of two sheets${(x,y,z) \in \mathbb{r}^3};