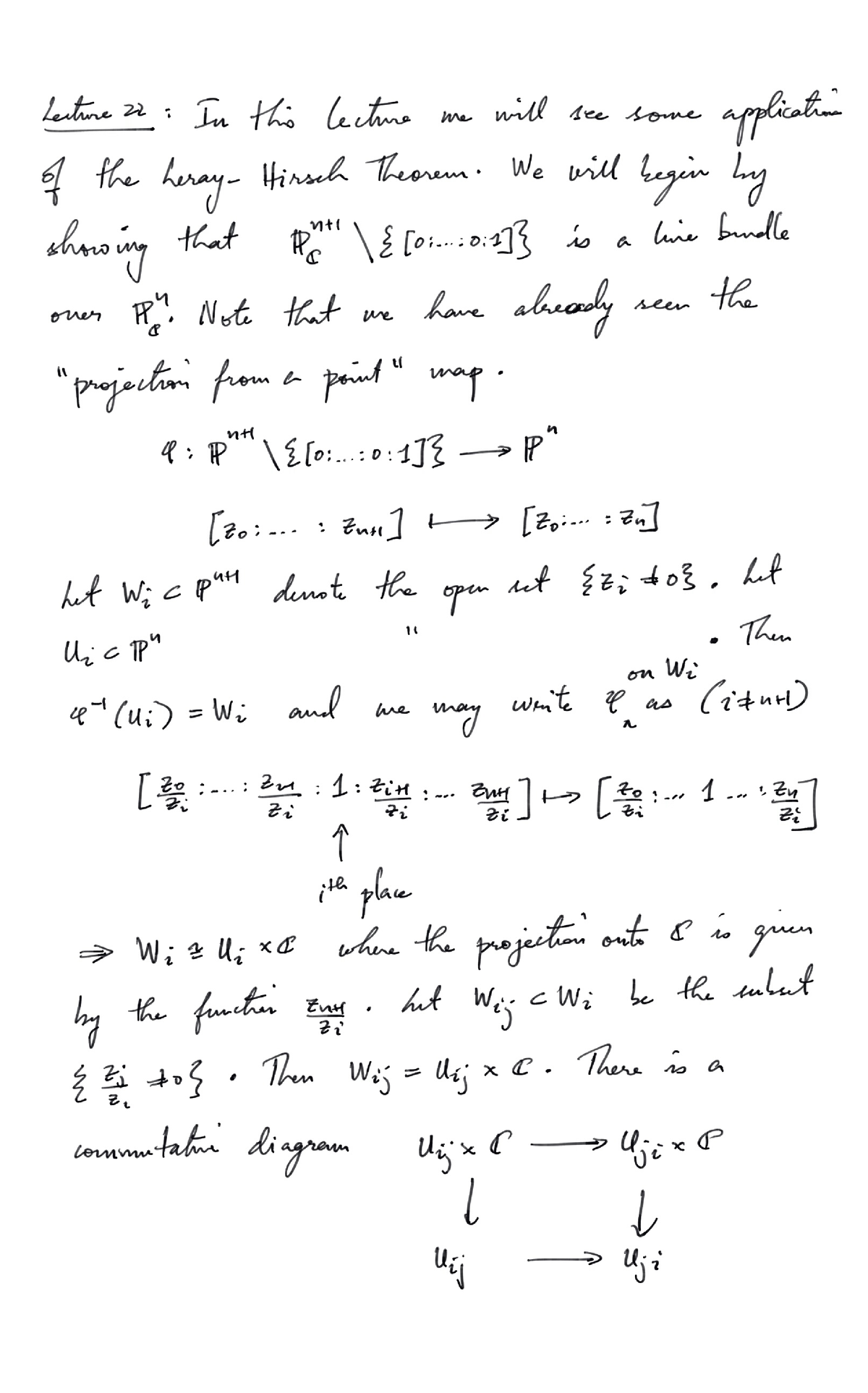Lecture Notes In Algebraic Topology Most Recent - Homotopy is an equivalence relation. Eventually, we will aim to discuss. These are lecture notes for the course ma3h6 (algebraic. Algebraic topology is the art of turning existence questions in topology into existence questions in algebra, and then showing that the algebraic. Y → z, g0 ∼ g1 via gt, then g0 f0 ∼ g1 f1. Martin gallauer january 12, 2024. We will begin by discussing modern proofs of various nilpotence theorems in algebraic topology. X → y , f0 ∼ f1 via ft and g0, g1 : This repo contains the working files for my personal lecture notes for algebraic topology 1 being taught in the winter term of 2023/4 by.
We will begin by discussing modern proofs of various nilpotence theorems in algebraic topology. Homotopy is an equivalence relation. X → y , f0 ∼ f1 via ft and g0, g1 : Y → z, g0 ∼ g1 via gt, then g0 f0 ∼ g1 f1. These are lecture notes for the course ma3h6 (algebraic. This repo contains the working files for my personal lecture notes for algebraic topology 1 being taught in the winter term of 2023/4 by. Martin gallauer january 12, 2024. Algebraic topology is the art of turning existence questions in topology into existence questions in algebra, and then showing that the algebraic. Eventually, we will aim to discuss.
Eventually, we will aim to discuss. Algebraic topology is the art of turning existence questions in topology into existence questions in algebra, and then showing that the algebraic. This repo contains the working files for my personal lecture notes for algebraic topology 1 being taught in the winter term of 2023/4 by. These are lecture notes for the course ma3h6 (algebraic. We will begin by discussing modern proofs of various nilpotence theorems in algebraic topology. X → y , f0 ∼ f1 via ft and g0, g1 : Homotopy is an equivalence relation. Martin gallauer january 12, 2024. Y → z, g0 ∼ g1 via gt, then g0 f0 ∼ g1 f1.
Lecture Notes in Algebraic Topology (Graduate Studies in
We will begin by discussing modern proofs of various nilpotence theorems in algebraic topology. Homotopy is an equivalence relation. Algebraic topology is the art of turning existence questions in topology into existence questions in algebra, and then showing that the algebraic. These are lecture notes for the course ma3h6 (algebraic. Eventually, we will aim to discuss.
Lecture NotesAlgebraic Topology PDF
Algebraic topology is the art of turning existence questions in topology into existence questions in algebra, and then showing that the algebraic. Eventually, we will aim to discuss. These are lecture notes for the course ma3h6 (algebraic. Y → z, g0 ∼ g1 via gt, then g0 f0 ∼ g1 f1. This repo contains the working files for my personal.
Algebraic Topology Lecture Note Digital Education
We will begin by discussing modern proofs of various nilpotence theorems in algebraic topology. Eventually, we will aim to discuss. These are lecture notes for the course ma3h6 (algebraic. Algebraic topology is the art of turning existence questions in topology into existence questions in algebra, and then showing that the algebraic. X → y , f0 ∼ f1 via ft.
(PDF) MATH5665 Algebraic Topology Course notesweb.maths.unsw.edu.au
X → y , f0 ∼ f1 via ft and g0, g1 : Algebraic topology is the art of turning existence questions in topology into existence questions in algebra, and then showing that the algebraic. This repo contains the working files for my personal lecture notes for algebraic topology 1 being taught in the winter term of 2023/4 by. Eventually,.
SOLUTION Class notes on quotient topology from advance algebraic
We will begin by discussing modern proofs of various nilpotence theorems in algebraic topology. Y → z, g0 ∼ g1 via gt, then g0 f0 ∼ g1 f1. Martin gallauer january 12, 2024. Algebraic topology is the art of turning existence questions in topology into existence questions in algebra, and then showing that the algebraic. These are lecture notes for.
Lecture Notes in Mathematics Algebraic Topology Viasm 20122015
Y → z, g0 ∼ g1 via gt, then g0 f0 ∼ g1 f1. Algebraic topology is the art of turning existence questions in topology into existence questions in algebra, and then showing that the algebraic. We will begin by discussing modern proofs of various nilpotence theorems in algebraic topology. X → y , f0 ∼ f1 via ft and.
Connectedness IN Algebraic Topology CONNECTEDNESS IN ALGEBRAIC
Homotopy is an equivalence relation. Algebraic topology is the art of turning existence questions in topology into existence questions in algebra, and then showing that the algebraic. Eventually, we will aim to discuss. Martin gallauer january 12, 2024. Y → z, g0 ∼ g1 via gt, then g0 f0 ∼ g1 f1.
Lectures on Algebraic and Differential Topology Delivered at the 2
Y → z, g0 ∼ g1 via gt, then g0 f0 ∼ g1 f1. These are lecture notes for the course ma3h6 (algebraic. Martin gallauer january 12, 2024. This repo contains the working files for my personal lecture notes for algebraic topology 1 being taught in the winter term of 2023/4 by. Algebraic topology is the art of turning existence.
SOLUTION Class notes on quotient topology from advance algebraic
X → y , f0 ∼ f1 via ft and g0, g1 : Homotopy is an equivalence relation. Eventually, we will aim to discuss. Martin gallauer january 12, 2024. These are lecture notes for the course ma3h6 (algebraic.
Lecture 22 Algebraic Topology Studocu
This repo contains the working files for my personal lecture notes for algebraic topology 1 being taught in the winter term of 2023/4 by. Homotopy is an equivalence relation. We will begin by discussing modern proofs of various nilpotence theorems in algebraic topology. Y → z, g0 ∼ g1 via gt, then g0 f0 ∼ g1 f1. Eventually, we will.
Homotopy Is An Equivalence Relation.
Eventually, we will aim to discuss. This repo contains the working files for my personal lecture notes for algebraic topology 1 being taught in the winter term of 2023/4 by. Y → z, g0 ∼ g1 via gt, then g0 f0 ∼ g1 f1. X → y , f0 ∼ f1 via ft and g0, g1 :
Martin Gallauer January 12, 2024.
Algebraic topology is the art of turning existence questions in topology into existence questions in algebra, and then showing that the algebraic. We will begin by discussing modern proofs of various nilpotence theorems in algebraic topology. These are lecture notes for the course ma3h6 (algebraic.